A spatiomaterialist theory of basic particles. The basic particles of physics are described by mathematical theories, which have been accepted as the best efficient-cause explanation of precise, surprising measurements, and they constrain what can be said about basic particles in many subtle ways. What I will present here is, by contrast, a mostly geometrical story about the basic particles, or rather, the beginnings of a geometrical theory. It comes from using spatiomaterialism and its explanation of other parts of physics to constrain further our beliefs about the basic particles. They must be constituted by bits of matter that coincide with space in some way or another, and since space has a three dimensional geometrical structure with an inherent motion connecting all the parts of space in time, these most basic forms of matter must have a spatio-temporal structure of some kind. What is presented here is one way that could be true. There may be other ways it could be true. And the one presented here is merely the model for a set of more specific theories that may be elaborated in different ways. My purpose is to show how adding the ontological constraints of spatiomaterialism to the mathematical constraints of the standard model opens up the possibility of a geometrical model of the basic particles.

It is, once again, an ontological explanation of why current theories about the basic particles are true, and its advantage over purely mathematical theories is that it reduces the number of basic assumptions that need to be made. To be sure, spatiomaterialism makes a big assumption that contemporary physics does not make — that space is a substance enduring through time, indeed, one with an inherent motion. But that will enable us to reduce the 37 particles recognized as basic by contemporary physics to, at most, only ten particles. Or even fewer, it might be argued, though that issue can be put off until we discover whether such ontologically based speculation is useful.

The ten basic particles we shall postulate are the photon, the three weakons, W^-, W⁺, and Z⁰, three neutrinos, electron, muon and tau, and their three antineutrinos. In one way or another, each involves a new assumption about the nature of matter, space and how they are related.

But it is conceivable that the photon can be explained as another form of weakon, and the six neutrinos may be just properties of space, that is, aspects of its relationship to weakon. Hence, a spatiomaterialist world may be made of nothing but space and three kinds of weakons.

This explanation of the nature of the basic particles is based on the assumptions we have already made about the nature of matter in order to explain the truth of the basic laws of classical physics, relativity theory, and quantum mechanics. Quantum matter is ultimately constituted by quantum events, which are basic and can coincide with space in various ways, and since they are cyclic, they constitute bits of matter that endure through time. The total energy or mass of a bit of quantum matter is simply the number of quantum cycles per second that constitute its existence. Since the photon is the simplest and plainest form of quantum event that we considered, let me recall what has been said about it.

An independently existing photon is a complete cycle of electric and magnetic forces. Those forces interact in a way that enables them to be repeated indefinitely. But since each cycle is a quantum event with the size of Planck’s constant, h, it either occurs as a whole or not at all. The total energy, or matter, in a photon depends on the number of cycles per second, as required by the physical law, E = hf. But the photon coincides with space in a way that makes it move with the inherent motion in some direction of space. Thus, it also has a wavelength, l, which is inversely proportional to its momentum, as required by the equation, p = h/l.

The photon has an intrinsic spin of 1, which implies that there are three different ways it could be oriented in a magnetic field. Two faces have a magnetic moment, positive or negative, corresponding to the two ways that light can be polarized. (If you follow the photon through space, the electric force rotates around to the right or left in space, which determines it circular polarization, but the difference between these properties is quantum mechanically equivalent to photons being polarized in mutually perpendicular directions as they pass through a filter.) And the third way that a spin 1 boson can interact in a magnetic field involves having no magnetic moment at all, as if there were a face in which the two possible orientations of spin were perfectly balanced. But the photon apparently loses the ability to interact from that “zero face,” as I will call it, because it is moving through space with the inherent motion.

Though the photon has energy, it has no rest mass. It might make it seem that its energy must come from its motion across space, like a form of kinetic energy. But that is not quite right, if its motion is due to the inherent motion in space. We are assuming that its energy comes from the cycles of quantum actions that are carried out by the exertion of electric and magnetic forces.

The photon is the gauge boson of the electromagnetic field, and on our ontological interpretation of gauge field theories, that means that electric and magnetic forces arise from space to act on a particle with an electric charge when it moves across space. At rest, the charged particle is a pulsating force in the surrounding space, which is synchronized with the pulsations of particles with the same charge throughout the universe (and 180⁰ out of phase with the pulsations of particles with the opposite charge). Since a magnetic force is also involved, it is a complex pulsation, perhaps, with internal cycles in two different planes. The electric and magnetic forces that arise from space to keep its pulsations in synch as the charged particle moves across space are the electric and magnetic forces, which were described by Maxwell. They are the same forces that can be coupled and exist independently as photons (for example, as a result of charged objects oscillating back and forth, as in antennas).

The photon introduces most of the properties that basic objects have, and in order to explain the other basic particles, we must postulate the existence of two other varieties of particles, weakons and neutrinos. All the other particles, both charged leptons and quarks, will be explained as combinations of neutrinos and weakons. The interaction between them is the weak force, on this ontological theory.

Weakons. The nature of weakons can be described in much the same terms that were used to describe the photon above. Weakons are also spin 1 bosons, for they are the gauge particles of the weak force. Given or theory about the nature of quantum matter, we assume that weakons are constituted by cycles of quantum events, and thus, what makes them different from photons is presumably coinciding with space in a different way.

Rest mass. One basic difference between photons and weakons is that weakons have a rest mass, whereas photons are massless. Indeed, weakons have a sizable rest mass, about 80,000 MeV/c² for the charged weakons and over 90,000 MeV/c² for the neutral weakon. That is nearly one hundred times the rest mass of the proton.

Rest mass is the property that made it impossible to explain weakons as the gauge particle of the weak field on the model of photons in the electromagnetic field, since gauge bosons are massless, according to Yang-Mills field theory. What makes Yang-Mills field theory so attractive is that particles interact the same way regardless of scale. They are, in other words, “gauge invariant.” But if one simply assumes that gauge particles have a rest mass, then the particles are no longer invariant under a gauge transformation. When the relevant particles are described on a much smaller scale, as if we were looking at them through a microscope, their mass decreases to the vanishing point. Mass in not gauge invariant.  

In order to give the gauge particle of the weak field a rest mass, therefore, physicists postulate another kind of particle, the Higgs boson, which is the gauge boson of yet another field. Unlike the weakon and the photon, which have a spin of 1, the Higgs boson has a spin of 0, meaning that it does not line up at all in the magnetic field. But it gives weakons a mass, only if Higgs bosons are located everywhere in space. Thus, it is assumed that the Higgs field is in a condition of least energy when there are Higgs particles everywhere. But the Higgs boson is a force with a certain strength (which enables the weakon to resist acceleration so that it tends to stay at rest), and so that is to say that the Higgs field has least energy when its force is strongest everywhere. This is paradoxical, because the energy associated with every other force of nature increases with the strength of the force.

Notice, however, that although this description of what gives the weakon a rest mass is paradoxical only when it is assumed that it is a description of matter. It is not paradoxical at all as a description of space. Space has no energy (it is not matter), but since it is a substance, it can exert a force. If the weakon’s relationship to space is what gives it a rest mass, it is not surprising that the force is exerted everywhere. Nor is it surprising that that is the condition of least energy, because it does not involve any energy at all. Thus, since we have already postulated the existence of space as a substance for other reasons, we can explain the rest mass of weakons without postulating Higgs bosons. We can take talk of Higgs particles to be a way of referring to space.

The function of the Higgs mechanism can be served by recognizing that quantum cycle have another way of coinciding with space. Instead of being picked up by the inherent motion and laying out their cycles as a certain wavelength in space, the quantum cycles of weakons have a purely rotational motion, and so they can be at rest in space. We assume that when quantum cycles coincide with space at rest, their matter has the form of rest mass, that is, the matter resists acceleration by a force. Weakons can, of course, be accelerated, and their rest mass determines, as we have seen, the scale of the quantum kinetic cycles that move these particles across space as time passes. But that role of rest mass comes from their relationship to space, not to Higgs bosons.

Like photons, weakons are bosons with an intrinsic spin of 1. That means that there are three different ways that a weakon and interact in a magnetic field. That means, as we shall assume, that each and every weakon has all three ways of interacting, and which way they interact depends on how they are oriented in the field. Taken geometrically, each way of interacting in a magnetic field can be pictured as a different face of the particle.

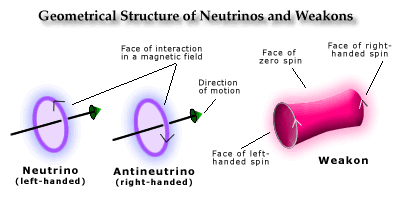
Two of the faces correspond to spin up and spin down, that is, having a positive or negative moment in the magnetic field. Each such face can be represented as a direction of rotation along an axis parallel to the direction of its motion, yielding two possibilities, left-handed spin and right-handed spin, as depicted in the accompanying diagram. These two faces are all that a particle with ½ spin has, and so as a first approximation, it could be represented as rotational quantum cycles of some kind which could be oriented in opposite directions relative to the magnetic field.

A spin 1 particle has a third face by which it can be oriented in a magnetic field in which it has no magnetic moment at all. But in the case of the weakon, we cannot hold that this zero face is lost by moving through space with the inherent motion of space, because weakons can be at rest. Instead, we have to admit that the weakon can interact in a way in which its two faces, with opposite orientations of spin, are somehow perfectly balanced. That suggests that we think of the weakon, not as a rotation which can interact only from either side of its axis, but as a rotating cylinder. If it is oriented so that one end is interacting with the magnetic field, it is rotating in one direction, and if it is turned around so that it interacts from with its opposite side, it is rotating in the opposite direction with a magnetic moment of the opposite sign. But if the cylinder interacts with the magnetic field from its side, it has no net rotation in the magnetic field, and its other faces are balanced against one another. That is how its zero face will be represented geometrically.

Electric charge. There are three kinds of weakons. Two have electric charges, with signs opposite to one another, and the third weakon is neutral. These are different kinds of weakons, not faces of each weakon. But given out assumption about the nature of the electromagnetic field, their charges can be explained as opposite ways of relating to the universal, electromagnetic pulsation, which is mediated by the inherent motion.

The electric charge is what is conserved by virtual photons, as the gauge bosons of the electromagnetic field. Since we are assuming that the forces of an electric charge are exerted in pulses that are perfectly synchronized with similar pulsations by other particles with the same charge wherever they are located in the universe, we can explain why like charges repel. And since opposite charges are 180⁰ out of phase, particles with opposite charge should attract one another. (We have also assumed that the pulsations have an additional complexity that accounts for the magnetic forces.)

These electromagnetic pulsations are independent of the rotational quantum cycles we have been describing in order to explain the three faces of spin orientation. Their intrinsic spin lines the particles up in a certain way in the magnetic field, but the direction of the electric and magnetic forces they feel depends on the gauge bosons that arise from the electromagnetic field in a way that keeps their pulsations synchronized as they move across space.

[We shall simply assume that weakons can have electric charges (and that they can exist without them), as a basic property of weakons. But there may be a simpler ontological explanation. Since weakons and photons are both constituted by quantum cycles, it is conceivable that the charged weakon is simply a photon at rest, or to take the weakon as basic, that the photon is simply a weakon that is moving across space. Though the weakon may have an electric charge when it is at rest, its zero face (without any magnetic moment) may be engaged with the inherent motion so that moves it across space at the velocity of light. In that case, it loses is rest mass and its electric charge is disengaged from the universal pulsation and becomes an electric force that is exerted in time with the rotations of its intrinsic spin, marking out the wavelengths of light. But when this particle is at rest, its cycles of electric forces are exerted from a point in space, and that geometrical configuration could be the radial field of the electric charge of the weakon, whose pulsations are synchronized with the pulsations of like particles everywhere. This would simplify the ontological explanation of basic particles even further, but I will leave it here as just a possibility.]

Weak charge. The weakon is the gauge particle of the weak force, and though it can act on other weakons, it needs fermions on which to act, and that is the role of neutrinos.

Neutrinos. The other kind of basic particle we must postulate is the neutrino, though as I suggested, it might be just an aspect of space in its interaction with weakons. The neutrino is a fermion, an opposite kind of particle from bosons, because it excludes other particles of the same kind from occupying the same quantum state (including location in space). Its spin of ½ means that it should have two possible orientation by which it can interact in a magnetic field, one face with a positive magnetic moment and another face with a negative magnetic moment.

Fermions can be represented geometrically as a rotational motion of some kind. From one side, a fermion would be rotating in one direction, whereas from the other side, it would be rotating in the opposite direction. There are, however, various kinds of rotation that could constitute a fermion, on this ontological theory, and let me emphasize that, though the frequency of the rotation or circular motion may vary, the magnetic moment is quantized. That is, the strength of the magnetic moment is a fixed quantity that does not depend on how fast it is rotating. That is just how basic particles coincide with space.

Varieties of neutrinos. Neutrinos differ from one another in two ways, by size and spin.

There are three sizes of neutrinos: the electron neutrino, which is the biggest, the muon neutrino, which is smaller, and the tau neutrino, which is the smallest of all three. It is not impossible that there are even smaller neutrinos, and I will suggest how they would be incorporated in this theory later. Furthermore, we shall assume that the spin of the neutrino is more like a motion around a circular pathway than it is the simple rotation of an object, and thus, the size of each kind of neutrino is the size of its circular pathway.

The spin of neutrinos are seen as problematic, because they violate the principle that fermions have two possible orientations by which they can interact in a magnetic field. Neutrinos have only a left-handed spin, that is, they rotate counterclockwise along an axis parallel to the direction of their motion. There are no neutrinos with a right-handed spin. Or at least, the weak force interacts only with left-handed neutrinos. (This is a violation of a symmetry recognized in particles, called “parity,” in which it is required that it also be possible for their structures and interactions to occur as if reflected in a mirror.)

The antineutrino, the antiparticle of the neutrino, however, does have a right-handed spin; that is, it rotates clockwise in the direction of its motion. Thus, for each neutrino, there is an antineutrino of the same size, but with the opposite orientation of spin. What is problematic about the spin of the neutrino is, therefore, that the distinction between being the same particle with the opposite orientation of spin and being the antiparticle breaks down in the case of the neutrino. That may be problematic mathematically, but it is not an ontological problem.

On this theory, neutrinos are special because they are elements that constitute other particles and, thereby, explain their properties, and it would not be surprising if the simplest particles do not have all the properties of the particles they explain. Thus, we will assume that neutrinos, as fermions, have two faces by which they can interact in a magnetic field, but that the opposite orientation of spin is also the antiparticle. Neutrinos have a left-handed spin along an axis parallel to the direction of their motion, whereas those with a right-handed spin are antineutrinos.

The reason the difference in orientation of spin gets confused with the difference between particle and antiparticle is that “antiparticles” is defined in terms of opposite electric charge, or “charge conjugation,” and we shall see how their opposite orientations in spin give neutrinos and antineutrinos different relationships to electric charges.

Relationship to space. Though I am counting neutrinos as basic particles, they will be explained ontologically in a way that may be come down to reducing them to an aspect of space. That is possible, because space is a substance, and its circular motion could be just an additional aspect of the inherent motion. Let us assume, accordingly, that there is at every point in space at least three kinds of motion that travel around in circles. Each goes both ways, and they are found in every plane of three dimensional space. There is a largest size for such circular pathways, which determines the longest period for a complete circuit, and circular pathways with shorter radii have shorter periods, with more complete circuits per second.

The idea is that there exists both a neutrino and antineutrino of all three kinds at every point in space. These circular motions are another aspect of space, like the inherent motion and presumably connected with the inherent motion in some way. Although these pairs of circular pathways do not have any linear motion through space (except for the motion of the inherent motion itself in a gravitational field), they do not have rest mass in space, because they are just parts of space itself.

We assume that there is an angular momentum associated with each circular motion, which would give it a moment of force in a magnetic field (explaining its intrinsic spin). That is to say that these circular pathways are oriented relative to the magnetic field. But since neutrino and antineutrino exist together, their angular momentums cancel out. They are neutralized, because they are circular motions in opposite directions. Thus, these circular pathways in space do not usually have any effect on what happens. Photons pass right through them, as do particles with rest mass, as if there was only space at that location.

This is to explain the neutrino ontologically in an opposite way from weakons. Unlike weakons, which have a rest mass that can be explained ontologically by the quantum cycles per second, neutrinos have no rest mass. At least, nothing in the theory requires them to have a rest, and experiments show that it cannot have more mass than about 12 eV/c². Thus, they may not even be constituted by quantum cycles, like forms of quantum matter. They could be simply aspects of space, because as we assumed, the magnetic field in which they are oriented is just an aspect of space (a form of force-field matter).

Interaction with weakons. Though neutrinos do not have an electric charge, they do have a weak charge. That is, they interact with weakons. But weakons exist only as pairs with opposite orientations of spin, and thus, we shall assume that the weakon can act on neutrinos by extracting one of these circular pathways from space and using it to travel around in circles. The weakon and the circular pathways are both oriented in the magnetic field, and when the weakon latches onto a such pathway with a circular motion in one direction, and it releases the pathway with opposite circular motion.

Since the released neutrino has no rest mass, it moves away from its former partner at the velocity of light. That is what physics assumes, though we shall explain its motion as due to the inherent motion in space. It engages with the inherent motion and thereby acquires the velocity of light. The released neutrino is just a bit of angular momentum that propagates through space, and it will not interact with anything, unless it runs into a weakon.

Weakons act on neutrino-antineutrino pairs where they are located, but how they act on such a pair depends on the charge of the weakon. A negatively charged weakon extracts a circular pathway with a left-handed circular motion relative to the direction of the magnetic field, and thus, it releases an antineutrino, that is, a neutrino with a right-handed circular motion. Correspondingly, a positively charged weakon extracts a circular pathway with a right-handed circular motion, and since that is an antineutrino, what it releases is a neutrino, which runs off with the inherent motion. The 180⁰ difference in the phases of pulsations of the positive and negative charges of weakons corresponds, therefore, to the right-handed and left-handed spins of neutrinos.

Charged leptons. This interaction between charged weakons and neutrinos affords an ontological explanation of charged leptons. The member of the neutrino pair that is retained by the weakon is used as a pathway to guide its own motion, transforming the weakon into a charged lepton, such as a tau particle, a muon, or an electron. Let us see how the properties of a charged lepton can be explained by this combination.

Electric charge. The weakon that interacts with the neutrino-antineutrino pair has an electric charge, and since electric charge is conserved, the charge is inherited by the lepton created by this weakon-neutrino interaction.

Negatively charged weakons extract neutrinos from space to use as their new pathway, and thus, negatively charged leptons contain a neutrino and they release an antineutrino. Positively charged weakons, on the other hand, extract an antineutrino for themselves and release the neutrino.

[It would be possible to formulate a theory like this by holding that the weakon simply acquires a new kind angular momentum from space and explaining the antineutrino as simply a form of angular momentum that remains in space as its way of conserving momentum. That might be a simpler theory, which emphasizes that neutrinos are just aspects of space, but it would leave out how space supplies the angular momentum that the lepton acquires as the weakon changes to a fermion. Thus, I will continue to describe the near basic particles as being constituted in part by neutrinos, if only to keep track of what space is contributing to their structures.]

The neutral weakon, Z⁰, does not interact with neutrino-antineutrino pairs at all. It mediates purely elastic collisions among particles with a weak charge. The electromagnetic pulsation of the electric charge is presumably what engages with space to extract neutrinos from them (suggesting that the circular motion of the neutrino and antineutrino is synchronized with the universal pulsation of negative and positive charges, respectively). 

Rest mass. Let us assume that the weakon interacts with the neutrino from its neutral face, that is, from the side of the cylindrical boson. Such a geometrical relationship is possible, since both particles are assumed to be lined up with the magnetic field. We have assumed that the cylinder is rotating, presumably with each rotation being a quantum cycle, so that the frequency of its quantum cycles explains its rest mass. It has a large rest mass, but if we assume that, when it interacts with a neutrino, its own rotation becomes a circular motion along the neutrino pathway, we can explain why the charged lepton has less rest mass than the weakon.

Since each circuit around such a circular pathway would take longer than one of the simple rotations that constitute the rest mass of the weakon, there are fewer quantum cycles per second in the new lepton, giving the composite particle a lower rest mass. But matter is conserved. The quantum cycles that previously constituted  the rest mass of the weakon do not drop out of existence, but rather are converted into quantum kinetic cycles, which give the new particle with a smaller rest mass a velocity relative to the inherent motion. (Momentum is conserved, because the antineutrino that takes off some direction in space with the inherent motion has an equal and opposite momentum.)

There are, however, at least three different sizes of circular pathways in space, and the smaller the circular pathway, the shorter the period and the greater the rest mass. Since a weakon has an enormous mass, it would usually become a tau particle or a muon before it became an electron. When a negatively charged weakon extracts a tau neutrino from space, for example, it releases a tau antineutrino. But since the muon and electron have longer pathways, requiring fewer quantum cycles per second, the tau particle can decay further. What remains of the negative weakon in the tau particle will release its tau neutrino, extract, say, a muon neutrino from space and release a muon antineutrino (with surplus matter converted to kinetic energy). Likewise, the muon would decay into an electron by releasing its muon neutrino, extracting an electron neutrino from space, and releasing the electron antineutrino to run off with the inherent motion. The electron is the last step, because it is the largest circular pathway possible in space, requiring the fewest quantum cycles per second. These are the decay patterns of weakons and charged leptons that have been found by physics, though they are explained here ontologically, by the size of the circular pathways provided by the neutrinos.

Spin. Intrinsic spin angular momentum is also conserved in the creation of a charged lepton, though in a curious way that might explain a couple of otherwise puzzling fact about leptons. The neutrino has no rest mass of its own, but when it is used as a pathway by a weakon, the composite particle acquires rest mass, which enables the lepton to be at rest in space. Thus, though free neutrinos lose one of their faces to the inherent motion, the captured neutrino can give the lepton it helps constitute a spin of 1/2 , with two faces from which it can interact in a magnetic field. With a weakon on its circular pathway, it has a rest mass and can turn around. Thus, it can be oriented in either way in a magnetic field. In one case, it will have a left-handed spin along an axis parallel to its motion in the magnetic field, and in the other case it will have a right-handed spin.

If the spin of the charged lepton comes from the neutrino, however, what happens to the other two faces of spin of the weakon? We have explained what happened to its neutral face. That is the face that the weakon uses to travel around the circular pathway (much as the photon uses its neutral face to travel along with the inherent motion). But the weakon had two other faces, one that give it a positive moment in a magnetic field and another that would give it a negative moment. These are represented by the two ends of the cylindrical structure of the spin one boson. The question is what happens to them.

Geometrically, the simplest explanation is that each of the weakon’s two non-zero faces coincides with one face of the neutrino in constituting the charged lepton. The circular pathway gives the charged lepton two opposite ways of being oriented in a magnetic field, because one of the non-zero faces of the weakon coincides with one face of the neutrino, and the other non-zero face coincides with the other one face of the neutrino.

To be sure, we have assumed that following the neutrino pathway requires the weakon to have fewer quantum cycles pre second, lowering its rest mass. It is as if the rotation of the cylindrical weakon were slowed down so that the weakon could follow the circular pathway provided by the neutrino. But the decrease in quantum cycles per second does not mean that its spin angular momentum is changed, because we are assuming that spin angular momentum is quantized. That is, the magnetic moment due to intrinsic spin is an all or nothing property: either the particle has it or not. Thus, the particle would have that same quantum property regardless of the frequency of the quantum rest mass cycles constituting it.

It may seem redundant or even gratuitous to suppose that the two non-zero faces of the weakon coincide with the two faces of the lepton. But it would explain one or two otherwise puzzling facts about leptons.

First, we know from Dirac’s equations that charged leptons, such as the electron, cannot be turned over completely by rotating them 360⁰, as one would expect, but requires two full turns. Since a 180⁰ rotation would make the face with the opposite orientation of spin in front, one would expect that two 180⁰ rotations would turn it back to its original state. Though a 180⁰ does give it the opposite orientation of spin, the equations imply that the electron has returned completely to its original size until it has been turned over twice, that is, 720⁰. That otherwise curious feature of the charged lepton would be explained ontologically on this theory, because turning it over completely would involve turning over not only the two opposite faces that the charged lepton derives from the neutrino’s circular pathway, but also the two opposite, non-zero faces that it derives from the weakon that is using that circular pathway.

Second, this ontological explanation of the charged lepton might explain another puzzling property. The electron has a spin of ½, as if its spin were only one-half of a quantum of action, and yet the magnetic moment that it exhibits in a magnetic field is more like what it would have, if it were a complete quantum of action, that is, about twice the expected strength. That could be explained, perhaps, by the way in which the spin of the charged lepton derives from the non-zero faces of the weakon. With a spin of 1, the weakon has a stronger moment in a magnetic field, when it has one at all, and that could be the source of the magnetic force of the charged lepton. This would be to interpret the “½” as just a device for cataloguing basic objects by the number of faces they can show for interaction in a magnetic field. (That is, according to quantum mechanics, the strength of the magnetic moment is the square root of the product of the spin and the spin-plus-one, or (s(s + 1))^1/2, and that means that the non-zero faces of the weakon have a magnetic moment equal to the square root of two times Planck’s constant, whereas the spin ½ particles has a magnetic moment equal to the square root of three divided by two times Planck’s constant.)

Decay patterns. As we have seen, this ontological explanation explains the decay patterns of the negatively charged weakon into the tau particle, muons and electron. It remains only to point out that it also explains the decay patterns of the positively charged weakon, and why decay stops there.

The positively charged weakon, W⁺, interacts in a magnetic field with the neutrino-antineutrino pairs in space, but it latches onto the circular pathway with a right-handed spin in the magnetic field, or the antineutrino, and it releases the neutrino, with a left-handed spin. Otherwise, the decay pattern is the same as described above, because the tau neutrino is the smallest, followed by the muon neutrino and, finally, the electron neutrino. The rest masses of the resulting positively charged leptons is inversely related to the sizes of their neutrino pathways.

The electron (or positron) is a stable particle, because it carries an electric charge, which cannot come apart, and there are no larger pathways in space than those provided by the electron neutrino (or antineutrino). We must take the conservation of electric charge to be a fact about how matter coincides with space, an aspect of the electromagnetic field whose gauge bosons exert forces that keep its pulsations in phase with other charged particles throughout the universe, on this interpretation of gauge field theories.

Quarks. Quarks cannot be explained in the same way as charged leptons, because weakons do not decay into quarks. Indeed, quarks are never found in isolation from one another. Hence, baryons, at least, must have existed from the beginning of the universe (or forever). But quarks can still be given a genuine ontological explanation in terms of the simpler particles of which they are composed, for their constitution could explain their properties and decay patterns. Though that would mean that quarks are not basic particles, the special configuration of more basic particles constituting them must have existed from the beginning, and that would be an ontological explanation of them. That is what is proposed here.

By contrast, attempts by physicists to explain quarks by a more basic structure focus on formulating a mathematical law from which both the electroweak force and the strong (i.e., color) force can be derived. This is the attempt to discover what is called the “grand unified theory,” or GUT, and though it is successful in some ways, it implies that there is a magnetic monopole and that the proton can decay. Neither phenomenon has been observed, and on this ontological theory, neither is possible. (Instead, the magnetic field is an aspect of space connected with the inherent motion by which particles are lined up according to their spin orientation to interact with one another, the protons may have a geometrical structure in space that literally cannot be undone.)

Quantum matter. The main idea of this theory of quantum matter is that bits of matter are constituted by cycles of quantum events in such a way that the quantity of matter in any object is equal to the total number of its quantum cycles per second. Such a nature is plain enough in the photon, whose motion across space with the inherent motion marks out its wavelength. And it has revealing implications in the case of the quantum kinetic cycles, which constitute the kinetic energy of particles with rest mass. But this nature is not so clear in the case of the particles with rest mass themselves, because their quantum cycles must somehow be contained by space in a way that does not involve motion relative to the inherent motion in space.

Weakons are a most elementary from of quantum matter, and so we have assumed that the weakon manages this trick by simply rotating like a cylinder, though, of course, with a fixed and unchanging number of quantum cycles per second (about 10²⁴ cycles per second, given its rest mass of 80,000 MeV/c² and a photon with an energy on the order of a few electron volts having a frequency of about 10¹⁵).

We have seen how charged leptons could be constituted by quantum cycles in which the weakon’s unit of action completes a circuit provided by a neutrino’s circular pathway. Each circuit takes so much longer than a simple rotation around it own axis that it reduces the total number of quantum cycles required each second to constitute the continued existence of the particle.

Quarks can also be explained as being constituted by a pathway for quantum cycles of the kind that derive from weakons. But the pathway must be more complex than leptons. The simplest way to explain why quarks cannot exist apart from one another is to hold that the pathway followed by their constituent quantum cycles depends on a combination of quarks. This is plausible, because physics has discovered that three quarks are required to make up a baryon, the only stable hadron, and each meson, the particle that mediates the strong force between them, is made up of a quark and an antiquark. As it happens, there is a way to explain these particles, their properties and decay patterns along the lines of the foregoing ontological explanation of charged leptons.

Twisted circular pathways. The key to the ontological explanation of quarks is, once again, the interaction between weakons and neutrinos. This is to interpret the weak force, not merely as the cause of decay patterns, but as the force that is responsible for their constitution. The weak force gives particles a nature by binding weakons to neutrinos. I have been describing this bond as a weakon moving along a pathway provided by a neutrino, and that is still the best way to represent it geometrically in the case of quarks. But even a single quark involves a more complex interaction between weakons and neutrinos than is found in charged leptons.

We must assume that the weak force can interact with two neutrinos. Such interactions are possible only when the neutrinos are of different sizes and one is a neutrino, while the other is an antineutrino. Moreover, it is an ordered interaction in which the two neutrinos play different roles. One neutrino is dominant, and the other neutrino is partially hidden. Such an interaction is what constitutes a single quark.

The interaction in a quark can be pictured in terms of a pathway provided for the weakon by the two neutrinos. What happens as the weakon moves along that pathway is that the weakon starts off moving around a circle in one plane, just as in a charged lepton, but the effect of the other neutrino is that the weakon winds up moving circularly in an orthogonal plane. That is, during each quantum event, the weakon follows a circular motion that is also twisted so that the plane of circular motion rotates 90⁰. That is not by itself a closed pathway for the weakon, but there are two different ways that the pathway can be closed — by the combination of quarks in mesons and baryons.

First, the weakon coming out of the twisted circular pathway one quark can enter the twisted pathway of an antiquark, and since the second quark rotates the plane of circular motion back to the initial plane of the first quark, the weakon can go around again and again. The second quark is able to complete the closed pathway because it is the mirror image of the first quark. That is the basic pattern of the meson. But notice that two weakons are required to constitute a meson. The complete pathway involves both a quark and an antiquark, and a complete quantum event is required for the weakon to traverse the pathway of each twisted circle. 

Second, it is also possible to put three of these twisting circles together as a closed pathway. In the first quark, the weakon follows a circular pathway which twists into a circular pathway in an orthogonal plane, and the second quark picks up the circular motion in that plane and twists it into a circular motion to the remaining plane which is orthogonal to both in three dimensional space. That is still not a closed pathway, but with a third quark that picks up the circular motion in that third plane and rotates it back to initial plane of circular motion in the first quark, the weakon can repeat the same trip over and over again. Since each twisting circle comes out in a direction perpendicular to its entrance, three of them together brings the weakon back to its starting point. This is the plan followed in baryons, composed of three quarks each. But three weakons are required to constitute such a particle, because one must be traversing each twisted circular pathways during each cycle. That is, three parallel series of quantum cycles constitute each baryon.

Weak interaction in each quark. This weak interaction in a quark between weakons and two neutrinos must, of course, be assumed as part of the nature of the weak force. It is a single quantum event, but it can be pictured in much the same way we did in the case of leptons.

Instead of interacting with the neutrinos by its zero face, the weakon could interact with both neutrinos at once, if it interacted by way of its two non-zero faces, each with an opposite orientation of spin in a magnetic field. That is, one non-zero face would try to follow the circular pathway of the neutrino, while the other non-zero face would try to follow the circular pathway provided by the antineutrino, and the combination of these two influences would result in a twisted circular pathway that rotates from one plane in three dimensional space to another.

This pattern would explain why the quark is constituted by a neutrino and an antineutrino, rather than two neutrinos (of different sizes). Since the non-zero faces of the weakon have opposite orientations of spin, the neutrinos with which they interact also have opposite orientations of spin.

A weakon interacting with a neutrino and antineutrino in this way would be contorted in a way that leaves its zero-face free, and that could become the face by which each quark exerts color forces on other quarks and passes its weakon on to the next quark. The eight different gluons might then be explained geometrically as the forces needed to line up three quarks properly (or to line a quark and antiquark) so that the weakon can complete a full circuit through them. Each quark must pick up a circular motion in one plane, twist it to another plane, and pass the circular motion onto another quark, and the gluons could be explained geometrically by their various roles in giving the three quarks the constant spatial relationship required for the weakons to make a complete their trips through the quarks. In other words, the color force would be another aspect of the weak force that is manifested when weakons interact with these neutrino-antineutrino combinations.

Notice that this account of the interaction between neutrinos and weakons parallels the explanation of leptons, for in that case, the interaction of the zero-face of the weakon with a neutrino exposed the two non-zero faces of the weakon, explaining the two non-zero faces of the charged lepton entailed by its ½ spin as a fermion.

[There may be other ways of picturing this interaction geometrically, though their explanations do not seem to be as complete. If the weakon uses its zero face, perhaps it begins in each quark by following the pathway of one neutrino, but in the presence of an antineutrino of a different size, it simply shifts to the second pathway, which twists its circular pathway. However, the quark seems to be a point-like object, and this theory does not explain its unity, since a sequential pathway would seem to require two quantum events. Furthermore, it does not explain why the interaction does not occur with two neutrinos of different sizes. Why is an antineutrino involved. (Notice that on the previous model, there is are reason for having both a neutrino and an antineutrino. Nor does it have any problem explaining why the neutrino and antineutrino are not of the same size, since a neutrino and antineutrino of the same size would annihilate one another.]

Kinds of quarks. If quarks are constituted by neutrinos and weakons in some such way, it is possible to explain all the kinds of quarks by the kinds of neutrinos of which they are composed. There are just enough differences between the composite particles to explain all the properties that distinguish one kind of quark from another, including their antiquarks.

Spin. As fermions, all the quarks have a spin of ½. We assume that the interaction between weakons and a neutrino and antineutrino of different sizes in each quark is a single quantum event. Together these more basic particles must make up a single fermion. As long as each weak interaction is a single quantum event, it is not impossible for a particle constituted this way to have a spin of ½, because the spins of the constituent neutrinos are not oriented in the same plane, where their spins would cancel one another out. Instead, the neutrinos are bound to one another in a way that we are assuming is unequal. One of the neutrinos making up the quark is dominant, as if the other neutrino were somehow hidden, and thus, the dominant neutrino’s orientation of spin can be assumed to be what gives the quark as a whole the two, opposite faces that fermions, with a spin of ½, must have.

There is one set of combinations of neutrinos with weakons that will explain all the kinds of quarks and their properties. Those combinations are indicated in the accompanying diagram (Constitution of Quarks). In each case, the first neutrino (or antineutrino) in each stack is the dominant one, tending to mask the other neutrino (or antineutrino).

Sign of electric charge. The d, s and b quarks all have an electric charge of –1/3, whereas the u, c and t  quarks all have a charge of +2/3. And antiparticles always have the opposite electric charge. The sign of the charge of the quark depends on the dominant neutrino in the same way that the sign of the charged lepton is determined. We assumed that the spin of the neutrino is synchronized with the universal pulsation of negatively charged particles and that the spin of the antineutrino is synchronized with the positive pulsation. That is how we explained why neutrinos acquire a negative charge, and antineutrinos acquire a positive charge. Accordingly, the charge of the quark is negative, when its dominant member is a neutrino, and the quark’s charge is positive, when the dominant member is an antineutrino (whatever ultimately explains the “dominance” of one neutrino over another in a quark).

Size of electric charge. The electric charge of the quark is either 1/3 or 2/3, and that can be explained as a result of the combination of the two neutrinos. We are assuming that the charge is a pulse of electric force that is synchronized with the universal pulsation of such charges, and thus, since negative and positive charges are 180⁰ out of phase with one another, the fractional charges can be explained by an appropriate rotation or phase shift in the cycle of such pulsations. It is presumably because a neutrino and antineutrino have opposite phases relative to that universal pulsation that the electric charge of the quark is in between –1 and +1, and so the relative sizes of the dominant and hidden neutrino could determine the size of the quark’s charge. That is, if the dominant neutrino is bigger (requiring fewer quantum cycles per second if it were on its own), then it is a charge of 1/3. But if the dominant neutrino is smaller (requiring more quantum cycles per second on its own), the charge is 2/3.

If the conservation of electric charge is due to the electromagnetic field, it is possible for the weakon traversing one of these twisted pathways to be separated from the electric charge it has when its exists independently, and it could even be what actually keeps the weak force from acting in ways that would not conserve charge (though there is probably a deeper explanation).

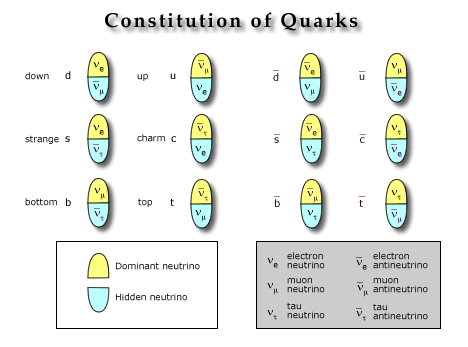
Rest mass. The rest masses of quarks are not well defined, because the quantities are not entailed by theory and the quarks cannot be measured apart from the baryons or weakons. It appears, however, that a good part of the rest mass of the baryon and meson comes from the gluons by which weakons pass from one quark to another, and since that matter presumably exist as potential and kinetic energy, the quarks are probably somehow in motion as the weakons are passing through them. Experiments do, however, suggest a range of rest masses for the quarks themselves, and the differences among them can be explained according to the theory of quantum matter.

The second family of quarks is more massive than the first, and the third family is more massive than the second. Moreover, in the second and third families, the quarks with 2/3 charge are considerably more massive than the quarks with 1/3 charge. These differences can be explained on the assumption that the rest mass depends on the total number of quantum cycles per second, because neutrinos with smaller circular pathways require more quantum cycles per second. Thus, the greater mass of later families can be explained by their use of smaller neutrinos: the tau neutrino replaces the muon neutrino in the second family and the muon neutrino replaces the electron neutrino in the third family. And the greater mass of the quark with 2/3 charge in the second and third families can be explained by the smaller size of the dominant neutrino.

Decay patterns of hadrons. The decay patterns of both baryons and meson can be explained by this theory of quarks. In a weak decay, one kind of quark turns into another kind, and this can happen in two ways. Either the dominant and hidden neutrinos switch roles, or they switch roles and one of the neutrinos is replaced by a larger neutrino (requiring fewer quantum cycles).

One pattern is the decay that occurs within each family of quarks. When a neutron decays into a proton, for example, the triplet of ddu quarks becomes a triplet of duu quarks, giving off an electron and an electron antineutrino (which is thought to be mediated by the decay of the negative virtual weakon released in the process). On this theory of quarks, what happens is that a d quark becomes a u quark, and that means that their neutrinos change positions. The muon antineutrino, which was the hidden member in the d quark, becomes the dominant member of the u quark, and the electron neutrino of the d quark becomes the masked member of the u quark. T

The same pattern occurs in the decay of mesons, which mediate the strong force among hadrons. For example, the negative pion is made up of a d quark and a u antiquark, and it typically decays into a negative muon and a muon antineutrino (by way of a negative virtual weakon). One of the ways this could happen is that the u antiquark becomes a d antiquark. That means that the electron antineutrino and the muon neutrino switch roles, and since that leaves the electron neutrino facing the electron antineutrino and the muon neutrino facing the muon antineutrino, they annihilate one another, and the weakon extracts a muon neutrino from space to become a lepton leaving a muon antineutrino as debris.

The weakon is just a virtual particle in these interactions. It is the gauge boson that arises from the weak field, that is, from space, according to the gauge field theory, to preserve the weak charges of the particles. For that role, the weakon does not need to have the energy of an independently existing weakon (any more than the virtual photon that mediates the electric and magnetic forces among electrically charged particles needs to have the energy of an independently existing photon). On this explanation, however, it is the weak charges of the neutrinos that are be preserved, and their weak charges are preserved by forces that line the neutrinos up as parts of the quark. Thus, the weak force can change the dominance roles of neutrinos in a quark (as long as electric charge is conserved). And any matter left over can act like a charged weakon on space to extract a neutrino and become a charged lepton (leaving the antineutrino as debris). 

The other pattern is the decay that occurs between families of quarks. The sigma minus is a baryon composed of the quark triplet, dds, and it typically decays into a neutron, with ddu, and a negative pion, which carries away the negative charge (and decays as described above). The decay of sigma minus requires an s quark to become a u quark. That involves not only a reversal of the roles of the two neutrinos in the s quark, so that the electron neutrino shifts from the dominant position in the s quark to the hidden position in the u quark, but also a replacement of the tau antineutrino in the s quark by a muon antineutrino as it takes up the dominant position in the u quark. Thus, this theory would imply that the decay of the sigma minus leaves two neutrinos in addition to the negative pion which is recognized, namely, the tau antineutrino that is released from the decay of the s quark and the muon neutrino that was also extracted from space in order to supply a muon antineutrino for the dominant position.

This other pattern also occurs in mesons. The positive kaon, for example, is a meson composed of a u quark and as s antiquark, and it typically decays into a positive muon and muon neutrino. Assuming that the neutrinos and antineutrinos must be lined up to annihilate one another, this requires the s antiquark to decay into a u antiquark, for then it can annihilate the u quark. That requires that the neutrinos in the s antiquark to switch roles and at the same time replace the tau neutrino with a muon neutrino (that is, the electron antineutrino gives up its dominant position in the s antiquark and takes up the hidden position in the u antiquark, and the tau neutrino from the hidden role in the s antiquark is replaced by the muon neutrino in taking up the dominant position in the u quark), Again there are two neutrinos as extra debris, because the s quark must not only release its tau antineutrino, but also extract a muon antineutrino in its place, releasing a muon neutrino.

All of the decays of quarks between families of quarks involve such additional neutrino debris, which are not recognized by high energy physics. But that is not an empirical reason for doubting that this theory is true, because neutrinos interact so weakly that they are almost impossible to detect. They cannot be monitored in particle accelerators. And this theory about the nature of quarks is not held by physicists.

Other families of leptons and quarks. It is possible, given this ontological explanation, that there are additional families of charged leptons and quarks. It would require a smaller neutrino and antineutrino. Call it “x”.

Charged leptons could be constituted by them and charged weakons in the same way as the electron, muon and tau particle (and their antiparticle). Their smaller size would require more quantum cycles per second, and that may be the reason they have not been observed, if they exist at all.

Given the role of neutrinos in constituting quarks, such a smaller neutrino would mean that there could be three more families of quarks. Consider the families of quarks with negative 1/3 charge, the d, s, and b quarks. Following their pattern, there could be such a quark composed of an electron neutrino and the x antineutrino, a muon and x antineutrino, and one with a tau particle and an x antineutrino. Similarly for the other members of each current family, there would be three new kinds of quarks, which could constitute baryons and mesons in the same way as currently recognized quarks.

The rules for constituting charged leptons and quarks make it possible to describe yet further families, if there are yet smaller neutrinos. 

Permanence of the proton. Contrary to theories currently circulating about the deeper structure of the basic particles of physics, this ontological explanation of their constitution by weakons and neutrinos implies that the proton never decays. That is the other side of the assumption that baryons must have been part of the universe from the beginning. Though their constitution can be explained, they cannot be taken apart.

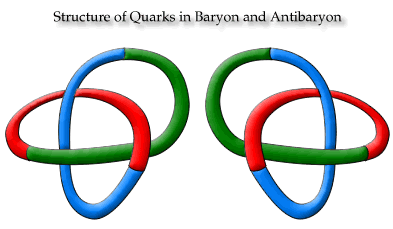
The structure of the baryon has been explained by holding that quarks have a structure that rotates a circular pathway in one plane of three dimensional space to another plane. Thus, three quarks rotate circular pathways through all three independent planes of three dimensional space in order to provide a complete pathway for weakons. This suggest that the pathway of weakons in the proton is a knot in three dimensional space that cannot be untied. (This model was suggested by P. W. Atkins, 1981., p. 86.) There are two such knots, and since they are mirror images of one another, they would correspond to the difference between baryons and antibaryons.

If, therefore, quarks can be explained by neutrinos and weakons in some such way, then given what has been said about the charged leptons, all the ordinary objects in space are explained ontologically. Physics recognizes 38 different basic particles, and we have seen how spatiomaterialism might make it possible to postulate only 10. It can explain the structure of ordinary material objects by starting with nothing but the photon, three kinds of weakons, and six kinds of neutrinos (three neutrinos and three antineutrinos). And as we have seen, the photon may be simply another form of the charged weakon, while the neutrinos may be just aspects of space that have to do with how space interacts with weakons. It may be possible to explain everything in the world by postulating nothing but space and three kinds of weakons. All the rest could be just how they work together to constitute the natural world.

Whatever the total number of basic particles that must be postulated, this ontological explanation of the basic objects of physics avoids having to believe that everywhere in the vacuum there are particles of every kind and their antiparticles. It is true that an energetic enough photon to create any particle and its antiparticle “out of the vacuum,” as they say. But it is not necessary to believe that all the various kinds of particles recognized by physics are contained everywhere in the vacuum, because if the vacuum is substantival space and it provides the neutrino and antineutrino pairs, all the different kinds of particles can be created together with their antiparticles from them and weakons, wherever there is enough energy.

To be sure, this ontological theory is speculative, and much more would have to be said to defend this theory of basic objects in detail. But the project of ontological philosophy would not be sunk, if this explanation of the basic particles of physics is not correct, because it is not necessary to give such an ontological in order to believe that the world is constituted by space and matter as substances enduring through time. I have included it, because it shows the power of spatiomaterialism to reorient our ways of thinking about physics and to open up new, more promising avenues of thought.

This covers all the basic issue of physics concerning the extreme of the very small and the brief, leaving only the extreme of the very large and long-lasting. In the same speculative spirit, let me suggest what this ontological explanation of the truth of the laws of contemporary implies about the beginning of the beginning, large scale structure, and end of the universe.