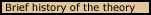A Brief history of Einstein’s special theory of relativity. The main conclusions of Einstein’s special theory of relativity are the Lorentz transformation equations. They are called the “Lorentz transformation equations,” because they had already been discovered, before Einstein’s first paper, by H. A. Lorentz, taking a Newtonian approach. That is where I will pick up the story about the Einsteinian revolution in physics, since spatiomaterialism is merely following in the footsteps of Lorentz. What I will call the four “Lorentz distortions”are sufficient to explain all the of the predictions by which Einstein’s special theory of relativity has been confirmed.

Lorentz. By 1887, some eighteen years before Einstein’s paper, Michelson and Morley had made experiments that showed that light has the same velocity relative to any object, regardless of its own motion. What made their result puzzling was the Newtonian assumption that the medium in which light propagates is a “luminiferous ether,” a very subtle kind of material substance that was supposed to be at rest in absolute space. Given that the velocity of light is everywhere the same relative to absolute space, they expected that the velocity of light, as measured from a material object, to vary with that object’s own velocity in absolute space—just as the velocity of ripples propagating in a pond arrive faster (or slower), when a boat is moving toward them (or away from them).

Michelson and Morley used an interferometer, which compares the two-way velocities of light in perpendicular directions; that is, light is reflected back from mirrors in perpendicular directions and the signals are compared to see if one is lagging behind the other. They made measurements at various points in the Earth’s orbit around the sun, where the Earth should have different velocities in absolute space. On a moving object, the time it takes for light to travel both to and from a distant mirror in the direction of absolute motion should be different from the time it takes to travel an equal distance in the transverse direction.^[1] The margins of error were small enough, given the velocity of light and the velocity of the Earth in its orbit around the sun, that it should have been possible for their interferometer to detect absolute velocity. But Michelson and Morley failed to detect any difference at all in the time it took light to travel the same distance in perpendicular directions. Absolute motion could not be detected.

Length contraction. The Michelson-Morley result was surprising, but even before Einstein published his special theory in 1905, Lorentz had proposed a Newtonian explanation of it. Lorentz showed, in 1895, that their result could be explained physically, if the motion of such an apparatus in absolute space caused its length to shrink in the direction of motion as a function of its velocity by a factor of . Lorentz argued that this length contraction is a real physical change in the material object that depends on its motion relative to absolute space.

The equation was L=L_o, where L_o  was the length at absolute rest. The shrinkage had been proposed independently by George F. Fitzgerald in 1889 and hence became known as the “Lorentz-Fitzgerald contraction”.^[2]

Lorentz tried to explain the length contraction physically, as an effect of motion through a stagnant ether on the electrostatic forces among its constituent, charged particles.^[3] But he could just as well have taken it to be a law of physics, making the Lorentz-Fitzgerald contraction the discovery of a new, basic physical law. (An ontological explanation of it will be suggested in the last section of this discussion of the special theory of relativity.)

Lorentz also described the length contraction as a mathematical transformation between the coordinates of a reference frame based on the moving material object and the coordinates of a reference frame at absolute rest. Lorentz started with the Galilean transformation by which Newtonians would obtain the spatial coordinates used on an object in uniform motion in the x-direction, or x’ = x - vt, and combining that with the length contraction he had discovered, he came up with the transformation equation, for obtaining the spatial coordinates on the moving material object.^[4]

Time dilation. There is, however, another distortion that material objects undergo as a function of their absolute motion. That is a slowing down of clocks (and physical processes generally) at the same rate as the length contractions, or the so-called "time dilation," which took somewhat longer for Lorentz to discover.

The Galilean transformation for time in Newtonian physics is simply t = t' , because Newtonian physics assumes that time is the same everywhere. But by using transformation equations to describe the distortions in material objects, Lorentz found that he had to introduce a special equation for transforming time: t’ = t - vx/c²  (Goldberg, p. 94). The new factor in the transformation equation, vx/c², implied that time on the moving frame varies with location in that frame. Lorentz called it "local time," but he did not attribute any physical significance to it. "Local time" is not compatible with the belief in absolute space and time, and Lorentz described it as “no more than an auxiliary mathematical quantity” (Torretti, p. 45, 85), insisting that his transformation equations were merely “an aid to calculation” (Goldberg, p. 96).

The slowing down of physical processes is called “time dilation.” Lorentz discovered this distortion by tinkering with various ways of calculating the coordinates used on inertial reference frames in relative motion. Thus, it is natural to describe time dilation as the slowing down of clocks on the moving reference frame. It was included in the final version of Lorentz's explanation, now called the “Lorentz transformation equations.” (Lorentz 1904) Those equations contained not only the length contraction and transformation for “local time”, but also the implication that clocks on moving frames are slowed down at the same rate as lengths are contracted (that is, ). The final Lorentz equation for time transformation included both the variation in local time and time dilation: .

Though Lorentz took the distortions that he discovered in fast-moving material objects to be laws of nature, he did not think that they were basic. He thought they were effects of motion on the interactions between electrons and the ether which could be explained by his electronic theory of matter, and he saw explaining this effect as the the main challenge to Newtonian physics. The transformation equations themselves never seemed puzzling to Lorentz, because he never took them to more than just a mathematical aid to calculation.

Poincaré. H. Poincaré thought he saw more clearly what Lorentz had discovered than Lorentz himself. As early as 1895, Poincaré had expressed dissatisfaction with Lorentz’s piecemeal approach, introducing one modification of the laws of Newtonian physics after another in order to account for different aspects of the phenomenon discovered by Michelson and Morley. Instead of such ad hoc modifications, he urged the recognition of what he called a “principle of relativity” to cover all the phenomena involved in fast-moving objects. As Poincaré put it in 1904, the principle of relativity requires that “the laws of physical phenomena should be the same for an observer at rest or for an observer carried along in uniform movement of translation, so that we do not and cannot have any means of determining whether we actually undergo a motion of this kind” (from Torretti, 83).

A principle of relativity like this had, in effect, been affirmed by Newton himself, when he admitted that his laws of motion depend, not on the absolute velocities of material objects, but only on their relative velocities. That is, Newton had already denied that absolute rest could be detected by mechanical experiments. It seemed that absolute motion could be detected only when Maxwell had discovered that light could be explained as an electromagnetic wave. Thus, Poincaré saw Lorentz's discovery of distortions in fast-moving material objects as a way of extending Newton’s principle of relativity to cover electromagnetic phenomena.

Understanding how the undetectability of absolute motion could be a result of the distortions that Lorentz had discovered, he referred to Lorentz theory as “Lorentz’s principle of relativity” even after Einstein had published his special theory and Lorentz himself was attributing the principle of relativity to Einstein (Torretti 85, Goldberg 212, and Holton 178). Indeed, Poincaré joined Lorentz in the attempt to explain the Lorentz distortions by the motion of material objects through absolute space, also expecting to find their cause in the dynamics of electrons; he also thought that motion through the ether caused material objects to shrink in the direction of motion and natural clocks to slow down by the exact amount required to mask their motion, as implied by Lorentz’s transformation equations (Goldberg 94-102, Torretti 38-47). Furthermore, Poincaré apparently thought that what Lorentz said about those equations in his 1904 work answered his own demand that it be a “demonstration of the principle of relativity with a single thrust” (Goldberg 214-15).

Lorentz's explanation of the distortions was not, however, a complete explanation of the principle of relativity. There are really two quite different aspects of the phenomenon described by the principle of relativity, and Lorentz had explicitly explained only one of them.

What Lorentz’s electron theory of matter (and Poincaré’s own refinements of it) explained physically were the Lorentz distortions in material objects with absolute velocity. That explained the negative outcome of the Michelson-Morley experiment: the contraction of lengths in the direction of motion and the slowing down of clocks as a function of motion through absolute space does make it physically impossible to detect absolute motion on a moving object by measuring the velocity of light relative to it. And that is one way in which inertial reference frames are empirically equivalent, because it holds of measurements made using any material object in uniform motion as one's reference frame, regardless of its motion through absolute space.

But there is more to the principle of relativity than explaining the null result of the Michelson-Morley experiment. The transformation equations that Lorentz constructed to describe the effects of absolute motion on material objects predict the outcomes of other experiments, such as attempts to measure directly the lengths of high-velocity measuring rods and the rate at which high-velocity clocks are ticking away. Though such experiments are more difficult to perform, they are conceivable, and Lorentz's equations do make predictions about them: moving measuring rods will be shrunken in the direction of motion and moving clocks will be slowed down. That suggests another way of detecting absolute motion. One might compare measuring rods or clocks that are moving at a whole range different velocities with one another and take the one with the longest measuring rods and quickest clocks to be closest to absolute rest. Hence, the principle of relativity would be false.

It is not possible, however, to detect absolute rest in this way, and as it happens, its impossibility is also predicted by Lorentz's theory, because he formulated his description of the Lorentz distortions in terms of transformation equations. Transformation equations are equations for transforming the coordinates obtained by using one material objects as a frame of reference into the coordinates obtained by using another material object as a frame of reference, and to be consistent, they must work both ways. That is, it must be possible to obtain the original coordinates by applying the transformation equations to the transformed coordinates. Thus, whatever distortions observers at absolute rest may find in material objects with a high absolute velocity will also be found by observers in absolute motion in material objects that are at absolute rest.

The recognition that Lorentz's theory, being formulated in terms of transformation equations, implied that all such inertial reference frames are empirically equivalent is presumably what led Poincaré to proclaim that Lorentz had finally explained the truth of the principle of relativity. Absolute rest and motion cannot be detected from any inertial reference frame.

Lorentz's theory was not, however, an adequate explanation of the principle of relativity, for there is still something puzzling about the empirical equivalence entailed by the symmetry of the Lorentz transformation equations.

Lorentz meant his transformation equations to be a way of describing the length contraction and time dilation in material objects with absolute motion, for that would explain the Michelson-Morley experiment, that is, why absolute motion cannot be detected by measuring the velocity of light in different directions. But since the transformation equations describe a symmetry between the members of any pair of inertial reference frames, they imply that observers using a fast-moving material object as the basis of their reference frame would observe a length contraction in measuring rods that were at absolute rest and a time dilation in clocks at absolute rest. That makes it impossible to detect absolute rest or motion by comparing different inertial reference frames with one another. But it is puzzling, because it is hard to see how both views could be true at the same time, that is, how two measuring rods passing one another at high velocity could both be shorter than the other and how two clocks passing by one another could both be going slower than the other.

In other words, Lorentz's theory does not really give a physical explanation of what Poincaré called the "principle of relativity." What entails the truth of the principle of relativity is the description of the Lorentz distortions in terms of transformation equations; the inability to detect absolute rest and motion by comparing inertial frames with one another comes from the symmetrical relationship that transformation equations represent as holding between the members of any pair of inertial reference frames. That symmetry is not physically possible, at least, not in the sense of "physical" that Lorentz had in mind when he tried to explain the distortions as occurring to material objects because of their motion in absolute space. If inertial frames are material objects in absolute space, then their measuring rods cannot both be shorter than the other and their clocks cannot both be slower.

As we shall see, what enables Lorentz's transformation equations to predict the symmetry of distortions is the "local time" factor in the time equation, vx/c², which Lorentz insisted was just an "aid to calculation." It represents the readings that would be given by clocks on a moving reference frame that have been synchronized by using light signals between them as if they were all at absolute rest, that is, on the assumption that the one-way velocity of light is the same both ways along the pathway between any two clocks (as required by Einstein's definition of simultaneity at a distance). That assumption is false, as Lorentz understood these phenomena, and clocks on the moving inertial frame would be mis-synchronized. It can be shown, as we shall see, that this way of mis-synchronizing clocks on a moving frame combines with the Lorentz distortions that the moving frame is actually suffering to make it appear that its own Lorentz distortions are occurring in the reference frame at absolute rest (or moving more slowly). This is a physical explanation, given how the other frame's measuring rods and clocks are measured. But it is an explanation of the principle of relativity that reveals it to be the description of a mere appearance. Though there is an empirical equivalence among inertial frames, a physicist who accepted Lorentz's Newtonian assumptions would insist that it has a deeper physical explanation.

It was not Lorentz, however, but Poincaré who declared that Lorentz had explained the truth of the principle of relativity, and Poincaré's acceptance of Lorentz's explanation as adequate may have been colored by his own philosophical commitment to conventionalism. Poincaré viewed the choice between Euclidean or non-Euclidean geometry as conventional, and he argued that convention is also what raised inertia and the conservation of energy to the status of principles that could not be empirically falsified. Poincaré's acceptance of the principle of relativity should probably be understood in the context of this more or less Kantian skepticism about knowing the real nature of what exists. Considering how the standard of simultaneity at a distance varies from one inertial reference frame to another (depending on the "local time" factor in the Lorentz transformation equations), the principle of relativity could also be seen as a conventional truth.

Poincaré's pronouncement that Lorentz's theory had explained the principle of relativity could not have set well with Lorentz himself. Lorentz may have continued to call it "Einstein's principle of relativity" because he realized that it was not explained by his theory about how spatial and temporal distortions are caused in material objects by their absolute motion. What is responsible for the principle of relativity is the symmetry in pairs of inertial frames entailed by his equations being transformation equations. If the distortions didn’t hold symmetrically in any pair inertial frames, it would be possible to detect absolute rest and motion. But to my knowledge, Lorentz never argued explicitly that what he called "local time" on the moving material object (that is, vx/c² in the time equation) represents a mis-synchronization of clocks on the moving frame that causes the moving frame's own Lorentz distortions to appear to be occurring in the other inertial reference frame.

The Newtonian explanation of all the relevant phenomena did not, therefore, have an adequate defender. Lorentz was more concerned to find an adequate physical explanation of the distortions he had discovered in material objects, and Poincaré was more interested in defending conventionalism. That is the Newtonian context in which Einstein's special theory of relativity won the day.

Einstein. Einstein took a dramatically different approach from both Lorentz and Poincaré. Instead of taking the principle of relativity to be an empirical hypothesis that could be explained physically by deeper, Newtonian principles, or as a conventional truth, Einstein raised the principle of relativity to the status of a postulate, which was not to be explained at all, but rather accepted as basic and used to explain other phenomena (Zahar 90-2). The mathematical elegance of Einstein's explanation of these phenomena is stunning. From the premise that all inertial reference frames are empirically equivalent, he derived a description of how two different inertial reference frames would appear to each other; that is, he deduced the Lorentz transformation equations.

Einstein's new approach can be seen most clearly by considering the structure of his argument. It is represented below in a diagrammatic form.

Einstein's Premises:	The Principle of Relativity	The laws of nature apply the same way on all inertial frames.
	The Light Postulate	The velocity of light is the same on all inertial frames.
	The Definition of Simultaneity  at a Distance	The local event halfway through the period required for light to travel to the distant event and back is simultaneous with the distant event.
Einstein's Conclusions:	To obtain the second frame's coordinates from the first frame:	To obtain the first frame's coordinates from the second frame:
Lorentz transformation equations      (kinematic phenomena)
Relativistic increase in mass      (dynamic phenomena)

The assumption that inertial frames are all empirically equivalent takes the form of three premises in Einstein’s argument: the Principle of Relativity, the Light Postulate, and Einstein's Definition of Simultaneity at a Distance (see table). Einstein's principle of relativity holds, with Poincaré, that the laws of nature hold in the same way on every inertial reference frame. That allowed Einstein to assume that Maxwell's laws of electromagnetism hold universally, and he considered what would be true of two different inertial frames in the same world. But in order to deduce the Lorentz transformation equations, Einstein also had to assume that that the velocity of light is the same relative to every inertial frame (the light postulate) and, accordingly, that simultaneity at a distance is defined on each reference frame as if the velocity of light is the same both to and back from a distance object.

What Einstein deduced from these premises are the “Lorentz transformation equations,” that is, equations for transforming the coordinates of any given inertial reference frame into those of any other.

The Lorentz transformation equations imply that any material object moving relative to any other inertial frame at a velocity approaching that of light will appear to suffer the Lorentz distortions: its clocks (and all physical processes) will be slowed down, and its measuring rods (and all material objects) will be shortened in the direction of its motion—both by the same amount, , which is a function of its velocity in the observer’s reference frame.

Einstein also inferred from these kinematic distortions and his principle of relativity that the mass of objects moving in an inertial frame increases at the same rate, making three distortions altogether. That dynamical implication is the source of Einstein's most famous equations, E = mc².

It should be emphasized that there are really two sets of transformation equations. It may not seem that way, because Einstein's conclusion is often stated as just one of the two sets of equations listed above, making it look mathematically simpler. But that formulation overlooks a mathematical detail and thereby obscures what Einstein's conclusion is about.

Though the Lorentz transformation is exactly the same both ways between the members of any pair of inertial reference frames, it requires two, non-identical sets of transformation equations, because their relative velocity has the opposite sign for each observer. That is, the two coordinate systems are set up so that their origins coincide when t = 0 and t' = 0, and since they are moving in opposite directions, the relative velocity is v for one of them and -v for the other. Thus, in order for the transformation to be symmetrical, one set of transformation equations has to have the opposite sign for the second factor in the numerator of the equations for space and time.

Since this seems to be a mere technicality, the conclusions of Einstein’s argument are usually represented as a single set of Lorentz transformation equations (the first set in the above table). Duplication is avoided by introducing a special mathematical symbol to make the single set of equations represent both transformations in any pair of inertial frames. Thus, Einstein's conclusion seems more like just another universal law of nature. But this is just homage to the Pythagorean ideal of mathematical simplicity, which obscures the fact that Einstein's theory is, in the first instance, about the symmetry that holds between the members of every pair of inertial frames.

It should also be emphasized that Einstein's theory is about how reference frames are related, and only indirectly about the material objects on which they are based. Though it does have implications concerning the relationship between material objects with a high relative velocity, that relationship is described by way of a mathematical transformation that holds between the reference frames based on them.

Inertial reference frames are based on material objects that are not being accelerated, and what makes the material object a reference frame is that it is used as the basis for a coordinate system by which the locations and times of events throughout the universe can be measured. (For this purpose, it is useful to think of an inertial reference frame as a grid of rigid bars extending wherever needed in space with synchronized clocks located everywhere.)

Notice that Einstein's three premises are all about reference frames based on material objects. Indeed, his definition of simultaneity prescribes how clocks must be synchronized to set up such a reference frame. The light postulate makes explicit the assumption about the velocity of light on which his definition of simultaneity is based. And the principle of relativity states that all the laws of physics will hold the same way within that reference frame as every other one, that is, will make correct predictions about what happens in that reference frame.

Einstein derives conclusions from his premises by assuming that there are two different inertial reference frames in the world and figuring out how they must appear to one another. Since his premises are about their reference frames, it is hardly surprising that his conclusion is about a mathematical transformation between their coordinates.

Indirectly, however, Einstein's conclusion is a description of how material objects with different constant velocities are related to one another as parts of the same world, since the reference frames in question are based on material objects. But to see Einstein's conclusion as a description of how material objects are related in space is to take Lorentz's approach. For Lorentz, these same transformation equations were just a mathematically convenient way of describing from the absolute frame the spatial and temporal distortions that occur in material objects with a high velocity in absolute space.

By calling his argument a theory of relativity, Einstein emphasized that his theory is about the empirical equivalence of all inertial reference frames, not the relationship between the material objects on which they are based. Observers on each inertial reference frame have their own view of the relationship between the material objects involved, but they are different views, and it is their views that are related by the Lorentz transformation equations. The symmetry of the relationship between their reference frames is what is crucial for Einstein, because that is what rules out any way of detecting absolute rest or motion by comparing inertial frames to one another and ensures that there is nothing to distinguish one inertial frame from another except their velocities relative to one another.

The Lorentz distortions in material objects are, however, a consequence of the Lorentz transformation equations that Einstein deduced. And if one does follow Lorentz, interpreting them as a way of describing the material objects on which the inertial reference frames are based, then the Lorentz transformation equations lead to paradoxes, as I have already suggested. Those equations imply that observers using any given inertial reference frame will find the Lorentz distortions occurring in the material objects on which the other inertial reference frame is based, and thus, the symmetry of the transformation for any pair of inertial frames leads to paradoxes.

Consider two inertial frames in motion relative to one another. From the first frame it appears that clocks on the second frame are slowed down. That would make sense, if from the second frame, it appeared that first-frame clocks were speeded up. But special relativity implies that it also appears from the second frame that clocks on the first frame are slowed down. That is, the distortions are symmetrical on Einstein’s theory, not the reverse of one another, as one might expect. And if the Lorentz distortions are really symmetrical, it is inconceivable that the two inertial frames are just material objects moving relative to one another in absolute space, because in absolute space, there can’t be two clocks next to one another both of which are actually going slower than the other. If one assumes that Einstein's theory is describing material objects, one must give up the assumption that those objects are located in absolute space. They are, of course, parts of the same world, but they must be related to one another in some other way.

The same problem arises from the symmetry of the length contraction and relativistic mass increase, for there cannot be two measuring rods passing one another in space that are both shorter than the other. Nor can there be two material objects both be more massive than the other. It is simply not possible for material objects located in absolute space.

None of this should be a surprise, however, because even the Light Postulate itself is incompatible with absolute space (or at least, with the assumption that light has a fixed velocity relative to absolute space). Though Newtonian physics had taken absolute space to contain the medium in which light propagates, Einstein assumed that the velocity of light relative to every object is the same, regardless of their own velocities relative to other objects in the world. Thus, Einstein held that the velocity of light would be the same in both members of any pair of inertial frames. This is not possible, if electromagnetic waves propagate through (an ether in) absolute space, like waves in water, for the motion of an object through waves propagating in space would change the velocity of those waves relative to the object—just as the motion of a row boat through ripples propagating in a pond changes the velocity of those ripples relative to the boat.

Taken as a description of the relationship between material objects in space, therefore, Einstein's special theory of relativity leads to paradoxes. But Einstein was not discouraged by these paradoxes. He was not thinking of inertial reference frames as material objects that are related in space, that is, in absolute space, or a space that is the same for both material objects. He was making a more abstract, mathematical argument and, in the process, giving physics a new standpoint from which to explain all physical processes.

That Einstein's basic approach is different from Lorentz's can be seen in what made Einstein curious about these phenomena in the first place. It was not the Michelson-Morley experiment, but rather something peculiar about the connection between classical mechanics and Maxwell’s theory of electromagnetism (Zahar 99-100). Einstein realized that even though Maxwell’s theory was standardly interpreted as referring to absolute space, absolute space was not needed in order to explain electromagnetic phenomena. For example, a conductor moving through a magnetic field at absolute rest moves electrons exactly the same way as if it were at absolute rest and the magnetic field were moving. That is what suggested the principle of relativity to Einstein, and though from it he derived the same transformation equations that Lorentz had proposed in 1904, Einstein claimed not to know about Lorentz's 1904 work.^[5]

By raising the principle of relativity to the status of a postulate, Einstein was assuming, in effect, that the deepest truth that can be known about the nature of space and time is that inertial frames are all empirically equivalent. And by relying on the predictions of measurements derived from that principle to justify his theory, Einstein had the support of the positivists, who dominated philosophy of science at that time. Indeed, Einstein admits to having been influenced by Ernst Mach at the time of his first paper on special relativity. To positivists, the paradoxes mentioned above about two clocks both going slower than the other and two measuring rods both shorter than the other are not real problems, but merely theoretical problems. Theoretical propositions that could not be spelled out in terms of observations were dismissed as "metaphysical," as if theories were mere instruments for making predictions. That attitude could be taken about the aforementioned paradoxes, because there is never any occasion in which two clocks can be directly observed both going slower than the other (or two measuring rods observed both shorter than the other). Observations are made from one inertial reference frame or another, and if both members of some pair of inertial frames are observed from a third reference frame, their clocks and measuring rods do not appear this way because of the Lorentz distortions that are introduced by its own velocity relative to them.

Though when taken as a description of material objects, the special theory of relativity is incompatible with the existence of absolute space, Einstein did not attempt to use its implications to show that absolute space does not exist. He was making a mathematical argument to show that accepted theories in Newtonian physics, which did assume the existence of absolute space, could all be replaced by theories that do not mention absolute rest or motion at all.^[6] All he explicitly claimed was that physics does not require an “absolutely stationary space” and that the notion of a “‘luminiferous ether’ will prove to be superfluous” because the “phenomena of electrodynamics as well as of mechanics possess no properties corresponding to the ideas of absolute rest” (Einstein, 1923 p. 37). It could be argued, therefore, that Einstein was merely imitating empiricist skepticism about theoretical entities generally by casting doubt on the reality of absolute space.

As it turned out, Einstein's theory proved to be remarkably successful in making surprising predictions of new experiments. For example, unstable particles have longer half-lives when moving at velocities approaching that of light. Clocks flown around the earth are indeed slowed down compared to clocks that stayed at home. The most famous new prediction of special relativity, E = mc², has been confirmed repeatedly. It is a consequence of the relativistic increase in mass, which Einstein first pointed out, and without it, high energy physics as we know it today would be inconceivable. Finally, the equations of special relativity have become (after Dirac) the foundation of quantum field theory as well as Einstein’s theory of gravitation. The Lorentz transformation is now so basic to physics that “covariance” (or “Lorentz covariance”) is taken as a constraint on all possible laws of physics.

To be sure, Newtonian physicists complained about the loss of intuitive understanding that came with the acceptance of Einstein's way of explaining these phenomena. It was no longer possible to construct in ordinary spatial imagination a picture of the nature of the world. But that objection did not detract from the predictive success of Einstein's theory, and the Einsteinian revolution made the capacity of mathematical arguments to make surprising predictions of precise measurements the establishment criterion for accepting theories in contemporary physics.

But physics is not just mathematics. A theory in physics is generally thought to be true when it corresponds to what exists, and if the special theory of relativity does not correspond to material objects in absolute space, we want to know what it does correspond to. The success in making surprising predictions of what happens by which Einstein's theory has been confirmed means that it corresponds to regularities that hold of change in the world, but it is natural to want to know the nature of what exists that makes those regularities true. The answer given by contemporary physics is spacetime, and it was Minkowski that has made that answer possible.

Minkowski. In 1908, Minkowski offered a mathematically elegant way of representing what is true from all inertial frames, according to Einstein’s special theory of relativity, using only the coordinates of any single inertial frame.^[7] His was a “graphic method” which he said allows us to “visualize” what is going on. The key to his diagram was to represent time in the same way as space, and that is what has led to the belief that what exists is not space and time, but rather spacetime.

In Minkowski’s “spacetime diagrams”, time is represented as a fourth dimension perpendicular to the three dimensions of space (though when comparing two inertial frames, the spatial dimensions can be reduced to one by a suitable orientation of their coordinate frames). A material object at rest in space is represented, therefore, as a line running parallel to the time axis, and a material object with a constant, non-zero velocity is represented by a line inclined slightly in the direction of motion. Units for measuring time and space are usually chosen so that the path of light in spacetime (the “light-line”, t = x/c) bisects the time and space axes, making the “basic unit” of distance how far light travels in a unit of time.

Since the second frame of reference is based on a moving object, we can think of the tilted line representing its pathway as its time axis. From such a moving reference frame, the location of an object at rest in the first frame (such as one always located at its origin) would change relative to the moving frame. So far, this diagram of space and time would be acceptable in classical Newtonian physics, because it represents a so-called Galilean transformation for the coordinates of moving reference frames (in which distances in space would be related as x' = x – VT, where v is their relative velocity in the x-direction.)

What Minkowski discovered was that the Lorentz transformation for moving reference frames could be represented by tilting the space line of the moving frame equally in the opposite direction and lengthening the units of time and space. That is, the time-line and the space-line of the moving frame are inclined symmetrically around the pathway of light. (See the comparison of the Newtonian Diagram of Space and Time and Minkowski's Spacetime Diagram.)

In either the Newtonian or Minkowski's diagram, every point represents the location of a possible event in space and time (called a “world-point”), and superimposing a second reference frame makes it possible to give such coordinates in either reference frame. From the coordinates for any event in the first reference frame, we can simply read off the coordinates for the same event in the moving reference frame, and vice versa. In the case of event E, for example, the coordinates in the first frame are (2,1), and in Minkowski's diagram, they are (1.3,0.3). All possible reference frames can be represented in this way, each with a different tilt to its time-axis representing its velocity relative to the first.

The two reference frames in the Newtonian diagram have a very simple relationship, because time coordinates are the same for both reference frames and there is no change in the units of either time or space. But Minkowski's spacetime diagram represents the Lorentz transformation, and not only are the units of time and space different, but the space-line of the moving reference frame is inclined relative to the first reference frame.

Minkowski’s spacetime diagram yields the same coordinates for the second reference frame that are obtained from the Lorentz transformation equations deduced by Einstein. Thus, it predicts that measurements of the second inertial frame will reveal its clocks to be slowed down and its measuring rods to be contracted in the x-direction.

But since the Lorentz transformation works both ways, it is possible to start with the second (tilted) reference frame and obtain coordinates for events in the first reference frame. Thus, it predicts that the moving observers will detect Lorentz distortions occurring in the first frame. This symmetry about the relationship between inertial reference frames makes it impossible to single out any particular frame as being at absolute rest by comparing reference frames with one another.

Minkowski's spacetime diagram may seem to mitigate the paradoxes resulting from the symmetry of the relationship between members of any pair of inertial reference frames, because it enables us to "picture" two clocks both ticking away slower than the other and two measuring rods both shorter than the other. It is just a result of how the inertial reference frames are related to one another.

But this wonderful power of Minkowski's spacetime diagram to represent these puzzling phenomena would not be possible, if the space-lines of different reference frames had the same slope. The inclined orientation of the space-line of the second inertial frame relative to the first frame is crucial to representing the Lorentz transformation, and it represents a disagreement between inertial observers about simultaneity at a distance. That is, observers using different inertial reference frames will disagree about which events at a distance are simultaneous with the origins of their systems when they pass by one another. That is the source of all the ontological problems with the belief in spacetime.

Though it is possible to interpret Minkowski's spacetime diagram as just a useful mathematical device for predicting the measurements that would be made on different inertial frames, that is what the Lorentz transformation equations already do. The historical significance of Minkowski's diagram is that it enables us to "picture" what exists in a world where Einstein's special theory of relativity is the deepest truth about the world. Thus, it leads to the belief in spacetime (that is, "spatiotemporalism," as I called it in Spatiomaterialism, or "substantivalism about spacetime," as it is called in the literature.)

The belief in spacetime comes from realism about special relativity. Scientific realism holds that theories in physics are true in the sense of corresponding to what exists, and spacetime is what must exist, if Einstein's special theory of relativity is the deepest truth about the real nature of what exists as far as space and time are concerned.

With regard to space and time, Newtonian realists would say that what their theories correspond to is absolute space and absolute time, that is, to a three dimensional space all of whose parts exists at the present moment and endure simultaneously through time. But that is not what Einstein's special theory of relativity corresponds to, because it implies that observers on all possible inertial reference frames are equally correct about the times and places of the events that occur in the world, even though they disagree about the simultaneity of events at a distance. What all the different inertial observers say about the times and places of events can, however, be true at the same time, only if what exists is represented by Minkowski's spacetime diagram. Thus, spacetime is the natural answer to the question about what corresponds to Einstein's special theory of relativity. According to realists about special relativity, what exists is spacetime, a four-dimensional entity that contains time as a dimension and, thus, is not itself in time.

Though Einstein may merely have been arguing in the spirit of the empiricist skepticism that prevailed in philosophy at that time, Minkowski made it possible to give a realist interpretation of Einstein’s special theory. His spacetime diagram showed how Einstein's theory could be interpreted as a description of what really exists in the case of space and time. Minkowski must have realized that he was giving a realist interpretation of Einstein's special theory of relativity when he introduced his spacetime diagrams; he said (Minkowski 75) that “space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality”. In any case, later in the twentieth century, when logical positivism gave way to scientific realism, Einstein’s skepticism about absolute space, if that is what it was, spawned the belief in the existence of spacetime. Indeed, regardless what Einstein may have believed in 1905, he apparently came to agree that what he had discovered was spacetime. (See Einstein 1966, pp. 205-8).

Scientific realism is, however, a way of letting science determine one's ontology. That is not the best way to decide which ontological theory to accept, because the empirical method that science follows is to infer to the best efficient-cause explanation, and that may not be the best ontological-cause explanation. But we can see how realism led to an ontology based on spacetime.

Einstein's special theory of relativity was a better efficient-cause explanation of the relevant phenomena than Lorentz's way of defending his transformation equations, because it made all the same precise predictions of measurements, but in a mathematically simpler way. As an efficient-cause explanation, however, all that Einstein's special theory requires is an empirical equivalence of inertial reference frames. It assumes that inertial frames are experimentally indistinguishable from one another, and it derives a description about how they must appear to one another as parts of the same world (where Maxwell's laws of electromagnetism hold). That relationship is described by the Lorentz equations for transforming their coordinates into one another, and it is represented by Minkowski's spacetime diagram. But Einstein's was a mathematical argument, and no mechanism or cause of the empirical equivalence was given.

A realist interpretation of special relativity goes beyond mere empirical equivalence and holds that inertial frames are all ontologically equivalent. If special relativity is the literal and deepest truth about the world, then what observers on all possible inertial reference frames believe must be true at the same time. That is to hold, not merely that no experiment can distinguish any one inertial frame from all the others as the absolute frame, but that there is nothing about the nature of any inertial frame that makes it stand out from all the others. That means, among other things, that no assertion made by observers on one inertial frame can be true unless the same kind of assertion made by observers on every other inertial frame is also true. (Nor can any assertion made on one inertial frame be false unless the same kind of assertion made on every other inertial frame is also false.)

The virtue of Minkowski's spacetime diagram is that it enables us to "picture" what exists in a world where inertial reference frames are all ontologically equivalent. Though it may still be unclear what spacetime is, Minkowski's diagram does allow us to believe that all possible reference frames are related to what exists in the same way, for it accommodates all possible standards of simultaneity at a distance. But they can all correspond to what exists only if the world is a four-dimensional entity all of whose parts in both space and time exist in the same way.

It is clear that this ontological equivalence of inertial frames is incompatible with absolute space and time, because if space and time were absolute, one inertial frame would be singled out ontologically from all possible inertial frames. Only one of all possible inertial frames would have the correct standard of simultaneity. Its location in space and time could be shared by observers on many other inertial frames, but none of their claims about which distant events are simultaneous with their shared here and how would correspond to what exists.

Einsteinians do not use the term "ontological equivalence" to describe the relationship between different inertial reference frames, but that is what the belief in spacetime comes to. Most philosophers of space and time simply take it for granted that they must accept "substantivalism" about spacetime in order to interpret the special theory as a description of the real nature of what exists. ^[8]

To believe in spacetime is to accept an ontology that is fundamentally different from Lorentz's Newtonian view, and the difference can be seen in what each implies about the nature of material objects.

Newtonian physicists assumed that material objects are substances that endure through time. They had to believe in absolute time, because the endurance theory of substances presupposes that only the present exists, or "presentism." (If the world is everything that exists, then objects that exist at only one moment in their histories must exist at the same time, for otherwise they would not be parts of the same world.) And since Newtonian physicists believed that material objects are all related to one another by (consistent) spatial relations, they were also forced to believe in absolute space. In a natural world, absolute time entails absolute space. Hence, the Newtonian world was made up of material objects in three dimensional space that endured through time.

Spacetime, on the other hand, is a four-dimensional entity. What exists is spacetime and all the events that are located in spacetime. Since time is an aspect of its essential structure, a spacetime world cannot endure through time. Thus, spacetime points and spacetime events must all exist in the same way independently of one another, if they exist at all. There are no material objects in a spacetime world, at least, not in the way that Lorentz believed. There are only the spacetime events that seem to make up the histories of so-called material objects. Thus, what is ordinarily called a "material object" is just a continuous series of spacetime events in spacetime. Its real nature is represented accurately by a “world line” in a spacetime diagram, because each spacetime event making up the history of a "material object" has an existence that is distinct from all the others, just as one point on a line exists distinctly from every other point on the line.

In short, whereas a material object in a Newtonian world exists only at each moment as it is present, but is identical across time, a so-called material object in a spacetime world is a continuous series of spacetime events, each of which exists eternally as a distinct part of the world. This is the difference between the endurance and perdurance theory of substances, and between the presentist and eternalist theory about time and existence.

Scientific realists sometimes assume that they can believe that Einstein's special theory of relativity corresponds to what exists without denying that they are themselves substances that endure through time by holding that only objects at a distance from themselves must exist the same way at all different moments in their histories. But that is not possible, if they believe that the truth of Einstein's special theory means that it corresponds to what exists for every observer. If Einstein's theory is universally true, then it must be true for inertial observers located elsewhere in the universe, and the only way that different inertial observes at a distance from us can all be correct about which moment in our local history is simultaneous with their passing by one another is if the moments in our local history all exist in the same way. We must perdure, rather than endure, because we are material objects at a distance for inertial observers elsewhere in the universe.

What Minkowski's “union” of space and time means ontologically is, therefore, that presentism is false. The denial of presentism is such a serious obstacle to an ontological explanation of the world that, in Spatiomaterialism, we were led to reject spacetime substantivalism (or "spatiotemporalism"), promising to justify it later by showing how it is possible for space and time to be absolute, despite the Einsteinian revolution. That is the argument we take up in the next section. But first, let us consider briefly why physics has ignored the ontological problems with eternalism.

What explains the ascendancy of the belief in spacetime is, once again, the empirical method of science and the physicists' addiction to mathematics as a means of practicing it. Behind Minkowski's spacetime diagram lies an elegant equation that has proved to be irresistibly attractive.

Minkowski provided a method of constructing in our own spacetime coordinate frame the spacetime coordinate frame that would be used by observers on an object moving relative to us. We may call their world-line the “moving timeline” (t = x/v), because it will be the time axis that moving observers use for their spacetime coordinate frame.

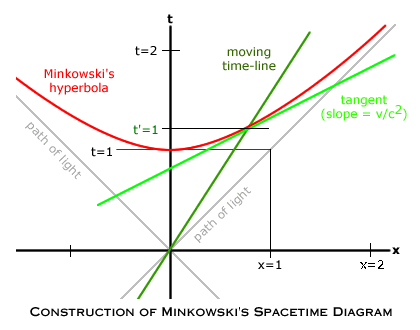
Minkowski formulated the conclusion of Einstein’s special theory as an equation that describes a hyperboloid in four dimensional spacetime: 1²  = c²t² - x² - y² - z². (When we orient our x-axis in the direction of the others’ motion, we can ignore the other two dimensions and it reduces to 1² = c²t² - x².) (It is the red curve in the diagram depicting how Minkowski's spacetime diagram is constructed.) The intersection of Minkowski’s hyperboloid curve with our time-axis is the unit of time in our frame (t = 1), and the unit of distance (in “basic units”) is the distance in our frame that light travels during that period of time (x = 1). The moving timeline (the time-axis of the moving spacetime frame) also intersects the curve described by Minkowski’s equation, and the distance of that point along our time-axis is the length of a unit of time on the moving coordinate frame according to our clocks.

As the diagram shows, moving clocks are slowed down in our frame. The other axis of the moving spacetime frame, the “moving space-line”, is also deduced from Minkowski’s equation. Moving space-lines all have the same slope as the tangent to Minkowski’s curve at the point of the moving timeline’s intersection with his curve. (Its slope is v/c²; the points on any line with this slope are simultaneous in the moving spacetime frame.) Finally, the unit of distance on the moving space-line is how far light travels in the moving frame during a unit of time on the moving frame.

Inertial frames are all equivalent on Minkowski’s theory, as on Einstein’s, since Minkowski’s equation determines precisely the same hyperbola in every moving inertial frame constructed this way in our own spacetime coordinate frame. That is, their hyperbolas all coincide. In particular, the same procedure on the moving coordinate frame, using the same equation (and taking the velocity to be -v along the x'-axis), produces the original coordinate frame. Or more abstractly, Minkowski’s equation can be generalized as a measure, s, of the separation between any two events that is the same in every inertial frame, despite variations in their coordinates for particular events: s² = c²t² - x² - y² - z².

In Minkowski’s equation, the parallel between the representation of space and time is remarkable. Time would be just another spatial dimension, except that it lacks a minus sign (and needs the velocity of light, c, to make units of time commensurable with distance). Indeed, that is how Minkowski includes relativistic mass increase. His equations’s form can be used to state the laws of nature that hold true in every inertial frame. In “four vector physics”, or “covariant” formulations of laws of physics, the energy of an object, E, takes the place of time and the three dimensions of momentum, p, take the place of the three spatial dimensions, so that the objects’ rest mass, m₀, rather than the separation, is what is the same about the object in all inertial frames: m_o²c⁴ = E² - p_x²c² - p_y²c² - p_z²c². The mathematics of four vector physics is so elegant and suggestive about the relationship of energy and momentum that it is not surprising that physicists now find themselves committed to the belief in spacetime.

By comparison with Lorentz’s ad hoc attempts to patch up classical physics in the wake of the Michelson-Morley experiment, Einstein’s argument was astonishingly simple and elegant, making it seem that Einstein had a deeper insight into these phenomena. And since Minkowski provided a diagram that made it possible to represent what special relativity implies about the world independently of particular reference frames, it is hardly surprising that the belief in spacetime has become the orthodox ontology in physics and the philosophy of science.

The acceptance of Einstein’s special theory of relativity involved, however, a remarkable change in the empirical method of physics, for it involved the abandonment of the requirement that explanations in physics be intuitively intelligible.

To follow the empirical method is to infer to the best efficient-cause explanation. Even in classical physics, theories were highly mathematical and confirmation was most convincing when they predicted surprising, quantitatively precise measurements. But since classical physicists still believed in absolute space and time, they also expected the best scientific theories to be intuitively intelligible, in the sense that it was possible to think coherently about what was happening in spatial imagination. But intuitive intelligibility was no longer possible when the best scientific theory required giving up the belief in absolute space and time. That was undeniably a loss, but physicists felt that they had to grow up and recognize that their deepest commitment was to judging the best theory by which is the simplest and most complete prediction of measurements. Since this came from mathematical theories, abandoning the requirement that physical explanations be intuitively intelligible left them addicted to mathematics.